Приращение функции

Уже совсем близко к пределам и интегралам! Но давай сделаем паузу – получим удовольствие от красивого решения математической задачи.

………………

Красивая задача:

Доказать неравенство:

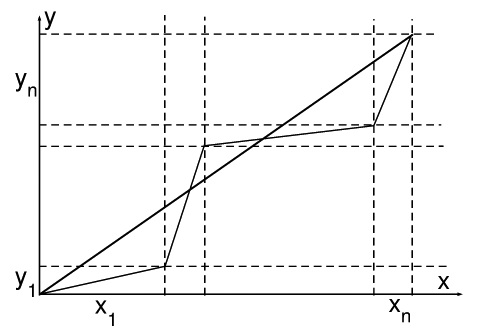
Кажется, что это ужасно сложно – наверное, надо все это возводить в квадрат, и можно только представить – какова будет в итоге мешанина. Но ведь это красивая задача, то есть для нее найдено красивое решение. Давай посмотрим на эту задачу, так сказать, геометрическими глазами. Что это вообще такое: √(x₁²+у₁²) ? Ничего не напоминает? Это ведь квадратный корень из суммы квадратов. Если x₁ – это длина одного катета прямоугольного треугольника, а у₁ – другого, тогда корень из суммы их квадратов – это длина гипотенузы. Значит, первая часть нашего неравенства – это сумма длин гипотенуз нескольких прямоугольных треугольников. А вторая часть неравенства – это длина гипотенузы одного прямоугольного треугольника, у которого длина одного катета равна сумме всех катетов x, а длина другого – сумма всех катетов у. Длина ломаной, проходящей от точки а до точки b, конечно же, не может быть меньше, чем длина отрезка, соединяющего эти точки напрямую, что и доказывает неравенство.

Этот рисунок поможет более ясно понять эту мысль:

……………….

Теперь идем дальше. Как мы уже знаем, прямая пропорциональная зависимость выражается формулой:

у = ах  , где а — некая постоянная величина. При увеличении х в два, к примеру, раза, у тоже увеличится в 2 раза и т.д. Постоянная а называется коэффициентом пропорциональности.

Введем теперь более широкое определение, частным случаем которого является прямая пропорциональность.

Линейной функцией называется функция вида:

у = ах + b

где а и b — постоянные.

Ясно, что если b=0 , то получается прямая пропорциональность.

Графиком линейной функции является прямая линия, что вполне очевидно, если вспомнить, что графиком функции  у = ах  является прямая линия. Чтобы график функции у = ах  превратить в график функции у = ах + b , надо к каждому значению у прибавить величину b, то есть, фактически, надо приподнять весь график на величину b. То есть – надо сдвинуть прямую вверх на величину b, что, конечно, не изменит ее формы – сдвинутая вверх прямая останется прямой.

Теперь введем одно важное понятие.

Пусть некоторая величина w переходит от одного своего значения w₁ к другому (конечному) значению w₂. Разность этих значений называют приращением величины w и обозначают ее как ∆w, т.е.:

∆w = w₂ — w₁

Понятно, что ∆w может быть как положительной, так и отрицательной величиной.

Обрати внимание – знак ∆w обозначает не перемножение какой-то величины ∆ на переменную w, а является слитным символом, обозначающим разность между наращенным значением переменной и ее исходным значением.

Когда независимая переменная х получает приращение ∆х, то ее функция у = f (x) тоже получает приращение:

∆у = f (x+∆х) — f (x)

Понятно, что приращение функции зависит не только от размера приращения аргумента, но еще и от того – каково начальное значение аргумента: представим себе функцию, график которой круто взмывает вверх в интервале 1< х <2, а затем идет полого. Если мы возьмем начальное значение х=1,5 и дадим ему приращение в одну десятую, то приращение функции будет значительно бОльшим, чем если бы начальное значение х было бы, скажем, равно трем.

Также ясно, что в случае линейной функции, крутизна графика которой везде одинакова (так как это прямая линия), размер приращения функции зависит только от размера приращения аргумента. Более того – эта зависимость прямо пропорциональная, то есть ∆у прямо пропорционально ∆х. Это может быть очевидным или неочевидным, но так или иначе, лучше это доказать, чтобы быть уверенным. Доказать это легко, просто записав значение линейной функции для х и для ∆х, а затем сравнив их.

Итак, сначала у нас есть: у=ах+b

Теперь х получила приращение, равное ∆х, после чего и у получила какое-то приращение ∆у. То есть мы имеем:

у + ∆у = а(х + ∆х) + b   или, открывая скобки по правилам умножения:

у + ∆у = ах + а∆х + b

Теперь поставим оба уравнения рядом – начальное и последнее:

у = ах + b

у + ∆у = ах + а∆х + b

В их левых и правых частях есть схожие элементы. Что, если их убрать? Тем более, что это приведет к тому, что не нужные нам х и у уберутся, а нужные ∆х и ∆у останутся.

Попросту вычтем из второго уравнения первое: из левой части второго уравнения вычтем левую часть первого, а из правой части второго уравнения вычтем правую часть первого. Можем ли мы вообще так сделать? Конечно можем. Я уже говорил, что из обоих частей одного уравнения можно вычесть одинаковые величины, и от этого уравнение не прекратит быть верным. Значит если мы возьмем второе уравнение, то из обоих его частей мы можем вычесть одно и то же, не нарушая равенства. Поэтому мы из левой части второго уравнения вычитаем левую часть первого, а из правой части второго уравнения вычитаем точно такую же величину: правую часть первого уравнения (ведь обе части первого уравнения равны).

То есть, если мы возьмем несколько уравнений и напишем их одно под другим, мы можем как угодно вычитать и складывать их левые и правые части, получая правильные уравнения. Мы можем также менять местами левые и правые части уравнений (он же равны) и снова складывать или отнимать левые и правые части разных уравнений.

Вернемся к нашей системе двух уравнений. Вычитая из второго уравнения первое (то есть из левой части второго уравнения вычтем левую часть первого и т.д.) получим:

∆у = а∆х

а это и есть – прямая пропорциональная зависимость.

Интересно пойти немного дальше и доказать, что если приращение какой-либо функции прямо пропорционально приращению аргумента и не зависит от его начального значения, то эта функция – линейная.

Действительно, это так. Сейчас мы исходим из условия, что ∆у = а∆х  для любого х.

Теперь зададимся вопросом — чему равно значение функции при х=0 ? Неизвестно, ведь мы же еще не знаем – какая это функция. Но чему-то ведь оно должно быть равно?? Конечно.  Обозначим это число как b. Итак,  f (0) = b

Дадим теперь аргументу какое угодно другое значение х, и функция получит тогда какое-то новое значение f(х), которое мы обозначим как у.

Теперь посмотрим: приращение аргумента ∆х равно х-0 = х, а приращение функции ∆у=у-b. Подставляя в исходное уравнение ( ∆у = а∆х )получим: у-b = ах  или  у = ах + b

Мне кажется, это очень изящное доказательство. Интересно – получится ли у тебя самостоятельно провести это доказательство? Ну хотя бы с третьего раза?:) Я советую это сделать, так как ты таким образом сможешь более ясно понять, как вообще производится это доказательство, каков ход мысли.

Из физики: процессы, описываемые линейной функцией, называются «равномерными».