Последовательность

Теперь мы можем ещё немного ближе подойти к интегралам.

«Последовательность» — тоже хорошо знакомое всем слово, но каково его точное математическое значение? Несколько чисел, написанных рядом? Несколько элементов, над которыми производятся какие-то операции? Хрен его знает. Муть. Избавимся от этой мути. Очень важно в точности понимать – что такое «последовательность», поэтому попробуй внимательно прочесть нижеследующее, возможно несколько раз, чтобы всё понять.

Говорят, что «функция определена при данном значении независимой переменной» (или, короче говоря, при данном значении аргумента), если этому значению аргумента поставлено в соответствие по какому-нибудь правилу одно или несколько значений функции.

Это очень просто. Например, возьмем функцию:

y = 2x

При х=5, мы получаем, что у=10, а это и значит, что функция определена при х=5.

Ну и теперь легко понять, что областью определения функции называется совокупность всех точек числовой оси, в которых функция определена.

Теперь дадим хитрое определение: функция  у = f (x) , у которой независимая переменная пробегает натуральный ряд чисел: х=1,2,3,4…, называется «функцией целочисленного аргумента».

Допустим, я беру первое целое число – «1», и ставлю ему в соответствие число 10. Затем беру второе целое число – «2», и ставлю ему в соответствие число 3. Третьему целому числу «3» я ставлю в соответствие дробное число 3/5. Четвертому – 8. Пятому – 11.

Таким образом, мы задали функцию целочисленного аргумента, так как каждому значению аргумента, являющемуся целым числом (то есть это 1, 2, 3, 4, 5), я поставил в соответствие определенное значение функции (10, 3, 3/5, 8, 11).

И далее:

Значения f (1) , f (2) , f (3) …, принимаемые функцией целочисленного аргумента, образуют последовательность, то есть, иначе говоря, совокупность, перенумерованную с помощью чисел натурального ряда и расположенную в порядке возрастания номеров.

Таким образом, ряд чисел, указанный выше (10, 3, 3/5, 8, 11), является последовательностью, так как, говоря проще, эти числа пронумерованы.

А что такое «пронумеровать»? Ну это и означает – поставить каждому определенному числу в соответствие какое-то одно целое число. Это на понятном, бытовом языке. Но это же самое можно сказать и на языке математики: «пронумеровать» — значит задать функцию целочисленного аргумента, когда каждому значению x, пробегающему значения от 1 и дальше, ставится в соответствие только одно определенное значение у.

Обратное тоже верно: любая последовательность является совокупностью значений некоторой функции целочисленного аргумента.

Не кажется ли тебе это слишком сложным, заумным? Нет, чтобы написать по-человечески: «последовательность — ну это когда рядом стоят некоторые числа». Так понятнее? На первый взгляд – да, а на второй – нет. А если я напишу числа вокруг какого-то числа, это будет последовательность? А если я напишу их в виде матрицы? А если несколько чисел будут написаны рядом, а потом – на расстоянии? А несколько графиков рядом, это последовательность? А система уравнений? Ничего не определено, ничего не ясно – полный хаос. Точные определения дают нам опору в ясности.

Теперь слово «пронумеровать» стало иметь определенный математический смысл, и это очень удобно.

Если какие-то числа написаны мною на листе бумаги вокруг какой-то фигуры, или по углам квадрата, или одно над другим или зигзагом – образуют ли они последовательность? Теперь легко ответить на этот вопрос: в определении последовательности не стоит никаких ограничений и указаний на форму записи её элементов – пиши хоть ручкой, хоть молоком, хоть по вертикали, хоть по синусоиде – не имеет значения. Важно другое – пронумерованы эти элементы или нет. Поставлено ли в соответствие каждому моему числу одно и только одно целое число от единицы и дальше? Если да, значит у нас есть последовательность. Если нет – то это просто набор чисел, не более того.

Сейчас, когда мы дали выше определение последовательности, мы всегда будем использовать это слово именно в таком значении, и ни в каком другом.

Приятно перебирать разные способы определения последовательности, имеющие один и тот же смысл. Например: последовательность – это значения, принимаемые функцией целочисленного аргумента. Представь себе, что это определение ты встретил бы где-то в книге до того, как прочел эту главу… а теперь – всё ясно.

Последовательность – это пронумерованная с помощью натуральных чисел совокупность чисел. Тоже понятно, если помнить – что такое «пронумеровать».

Последовательность — это такая совокупность чисел, каждому из которых поставлено в соответствие какое-либо число натурального ряда чисел – от единицы и дальше.

Последовательность можно задать просто вручную, пронумеровав те или иные числа так, как тебе угодно, а можно — с помощью функции.

Например, члены геометрической прогрессии:

1/2, 1/4, 1/8, 1/16… являются последовательными значениями функции  f(n) = 1/2ⁿ,n=1,2,3,4…

То есть члены геометрической прогрессии образуют последовательность. Геометрическая прогрессия – одна из разновидностей последовательности.

Легко представить себе – как выглядит график любой функции целочисленного аргумента. Поскольку эта функция определена только при значениях аргумента, равных 1, 2, 3 и так далее, то графиком будет не непрерывная линия, а совокупность отдельных точек, у которых абсцисса целочисленна, а ордината равна тому, чему она оказывается равна в соответствии с необходимыми вычислениями. Непривычный вид графика, конечно, ведь под «графиком» мы привыкли понимать какие-то линии, а тут – лишь точки! И все же это тоже график функции.

То, что нельзя смешивать понятие функции и понятие «графика функции» — понятно. Но обычно не понимают того, что нельзя также смешивать понятие «функции» с понятием «аналитического выражения функции»! Функцию мы можем задать аналитически, и при этом в одном интервале значений аргумента функция будет одной, а в другом – другой! То есть это будет вполне определенная функция, мы можем дать ей какое-то название, а определяться она при этом будет двумя, совершенно разными и несводимыми друг к другу аналитическими выражениями.

Если это не совсем ясно – проще будет на примере.

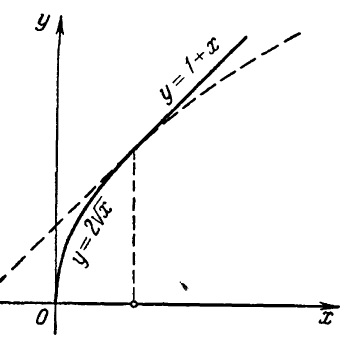
Зададим функцию у = f (x) так:

f (x) = 2√х         при 0 ≤ х ≤ 1 (при икс больше нуля или равно нулю и меньше единицы или равно единице)

f (x) = 1 + х       при х ˃ 1 (при икс больше единицы)

Этими двумя аналитическими выражениями задается однозначная функция, определенная при всех х ≥ 0, однако эта функция в интервале от 0 до 1, и в интервале от 1 до бесконечности представлена двумя совершенно различными выражениями. График этой функции см. ниже:

Таким образом, в этом примере функция задана двумя совершенно разными аналитическими выражениями (проще говоря – формулами), каждая из которых определена на определенном интервале значений переменной х.