Математика необходима в той или иной степени для любой науки. Иногда математические знания требуются в исключительно огромных количествах (как, например, в теории струн, в квантовой механике). Иногда достаточно лишь общих представлений в разных областях математики. Чаще всего оказываются востребованными познания в математическом анализе, теории множеств, линейной алгебре, поэтому начинать целесообразно именно с них. Я отлично понимаю, что у многих выработалась сильнейшая аллергия на математику благодаря школе, но нельзя же позволить каким-то глупым людям на всю жизнь лишить тебя удовольствия от изучения и понимания математики… Поэтому я предлагаю преодолеть привычное отторжение и попробовать еще раз.
В математике очень и очень нужны термины. Когда мы начинаем что-то исследовать и наталкиваемся на новые явления и закономерности, нам необходимо обозначать их терминами, чтобы мысль могла идти дальше. Это касается не только наук, но и бытовой жизни. Если я хочу попросить тебя включить телевизор, я говорю «включи телек», при этом не отдавая себе отчета в том, что «телек» — это короткий и удобный термин. Представь себе, что было бы, если бы мне пришлось говорить «включи электронное устройство для приёма и отображения изображения и звука, передаваемых по беспроводным каналам или по кабелю»! Впрочем, слово «изображение» тоже является термином, и вообще-то мне тогда следовало бы сказать так: «включи электронное устройство для приёма и отображения объекта, образа, явления, в той или иной степени подобного (но не идентичного) изображаемому, подобие которого достигается либо с помощью использования технологий, опирающихся на те или иные физические законы, либо результатом труда создателя изображения, а также звука, передаваемых по беспроводным каналам или по кабелю». Конечно, каждое слово в этом длинном предложении также является термином…
Никакое познание и даже никакая бытовая жизнедеятельность без терминов невозможна – это ясно. Поэтому в юриспруденции, математике, Селекции восприятий, кулинарии и вообще везде нам жизненно необходимы термины.
Это в общем понятно. Но следует понять и еще кое что. Так как роль терминов в нашей жизни поистине грандиозна, то очень важно ещё и понимать значение этих терминов совершенно точно. Если вместо расчески я возьму утюг, то что получится? Недостаточно точное понимание терминов является огромным препятствием в достижении ясности в любой науке. Возникающая муть отравляет все удовольствие полностью, до основания, так как лишает тебя возможности наслаждаться ясностью.
Обычно в учебниках термины вводятся как бы между делом, создавая впечатление, что они не так уж и важны. И совершенно напрасно. Я уверен, что задаче разъяснения значения того или иного термина необходимо уделять много внимания, чтобы исключить возможность неправильного понимания.
Для начала введем термин «параметр».
Например, я в горах нашел камень, и задумался — донесу я его до логова, или нет. Необходимо прикинуть – сколько он весит. Я беру его, приподнимаю – кажется, килограмм 12. Отлично, это немного, значит дотащу. Таким образом я примерно прикинул вес камня и сделал из этого полезный вывод.
Но этого еще недостаточно, чтобы я смог понять – точно ли получится у меня его дотащить до логова, ведь камень надо засунуть в рюкзак, надо чтобы он там поместился. Измеряя размеры камня, я понимаю, что в моем рюкзаке для него хватит места. Таким образом, я измерил ширину, длину и высоту камня и сделал из этого еще один полезный вывод.
Вес камня, его длина, ширина и высота – всё это является его признаками – то есть тем, что позволяет мне отличить его от другого камня. Кроме этих признаков существует и бесчисленное количество других. Цвет, форма, запах, вкус, прочность, растворимость, электропроводность, теплопроводность, интенсивность чувства красоты, возникающей тогда, когда я на него смотрю, цена, градиент цвета и прочее и прочее. Некоторые признаки мне в данный момент важны, некоторые – нет.
Вес, длину, стоимость на рынке – всё это и многое другое мы можем с той или иной точностью измерить или оценить. Если у меня есть линейка, то длину камня я смогу измерить с точностью до сантиметра. Если линейки нет, то придется удовлетвориться оценкой «на глаз», что уменьшит точность.
Теперь мы можем дать определение: термином «параметр» мы называем всё, что угодно, что подвергается какому-либо измерению или может быть измерено и выражено в числах, и отражает, таким образом, какое-либо свойство объекта.
Я могу измерить линейкой длину камня? Могу. Могу ли я оценить его длину на глаз? Тоже могу. Значит его длина – измеримая величина. Относится ли «длина» к самому камню? Конечно, ведь мы именно его длину замеряем. Отражает ли, таким образом, эта длина какое-то определенное свойство камня? Конечно. Значит, длина измерима и отражает его свойство, помогает нам отличить его от других камней. Значит, согласно определению, длина – это один из параметров камня.
Чем больше разных параметров какого-либо объекта мы измерим или оценим, тем более точное у меня будет о нём представление.
Яркость света можно измерить? Можно, значит и яркость может быть параметром. Глубину глупости человека тоже можно примерно оценить, поэтому глупость тоже является параметром.
При определении параметра мы использовали слово «измерение». На бытовом уровне нам понятно, что такое «измерить» — это значит оценить что-то, сравнивая его с каким-то эталоном. Даже если мы делаем это в своем воображении. Прикидывая «на глаз» длину камня, я примерно вспоминаю, как выглядит линейка длиной в 30 сантиметров, и в своем воображении я прикладываю эту линейку к камню и делаю свою оценку.
Простейшая форма измерения состоит именно в том, что некоторый объект, обладающий тем же свойством, что и измеряемый (в нашем примере, это свойство – длина), принимается за «единицу измерения», после чего мы вычисляем – сколько раз эта единица может быть уложена в измеряемом объекте. Например, бамбуковый ствол и моя ладонь тоже обладают свойством «протяженности в пространстве», или «длиной». Принимая длину своей ладони за единицу, я выясняю, что мне требуется 50 раз приложить ладонь к бамбуку, чтобы покрыть его от начала до конца. Отсюда я делаю вывод, что длина бамбука, выраженная в моих ладонях, равняется пятидесяти. Я измерил длину бамбуковой палки в своих ладонях. Моя ладонь стала единицей измерения. Если такие единицы измерения мне неудобны, я могу использовать другие, причем совершенно не обязательно, что это будет именно линейка. Например, я хочу поставить двадцать стульев вдоль стены помещения. Линейки у меня нет, зато есть стена и есть один стул. Этого достаточно! Я беру этот стул и ставлю его с одного края стены, делая карандашом отметку, где я мог бы поставить второй стул. Таким образом, передвигая свой стул, я выясняю, что длина стены примерно равна 21 стулу. Значит 20 стульев точно влезут, даже если я не очень точно проводил свои измерения. В данном случае один стул стал для меня единицей измерения длины стены.
Теперь, когда значение термина «параметр» стала ясна, можно получить удовольствие, читая другие определения, которые еще пять минут назад показались бы совершенно запутанными. Например – из википедии: «параметр — это величина, значения которой служат для различения групп элементов некоторого множества между собой». Мы можем поспорить о том – удачное это определение или нет. Если раньше мы говорили о параметре как о том признаке предмета, который «может быть измерен», то здесь говорится о том, что измерение это производится с определенной целью – чтобы отличить одну группу объектов от других. На самом деле цель совершенно неважна. Конечно, мы можем измерить длину карандашей и сказать, что все те, что короче 10 сантиметров, мы назовем «короткими» (то есть поместим их в условную группу «короткие»), а все те, что от 10 до 15 – средние, и остальные – длинные. Мы можем это сделать, конечно. А можем и не делать, а длина все равно останется параметром карандаша. Поэтому это определение я считаю неудобным, и даже неправильным. Мы можем провести такую оценку определения термина «параметр», потому что хорошо разобрались в том – что это такое вообще – параметр.
До сих пор мы брали объекты – камень, стул, ладонь – то есть что-то такое, длина чего постоянна. Но параметр может быть не только постоянной, но и переменной (или изменяющейся) величиной. Вес камня – величина постоянная, а вот, например, высота живой ёлки – нет. В Гималаях есть сосны с упругим, мягким стволом и с огромными, длиной по 15 сантиметров, мягкими иголками. В треке к Эвересту такие сосны в районе Гокьо довольно невысокие – метра 2-3, в районе Намче они встречаются уже высотой до 10 метров, а на подходе к Лукле уже растут гиганты высотой по 40-50 метров. Я выкопал десяток саженцев и посадил их в мордопоселении вдоль Большой Травяной Полянки, и мне стало интересно – как быстро они будут расти? Я измерил высоту саженца сейчас, и буду измерять её раз в полгода. Разумеется, по мере того, как сосна будет расти, ее параметр «высота» будет меняться, то есть он будет «изменяющейся величиной». То есть изменяющейся величиной называется тот или иной параметр, если его значение изменяется. При этом некоторые параметры могут меняться только в одну сторону – как, например, высота растущей ёлки. Другие параметры могут меняться то в одну, то в другую сторону. Но в любом случае, если параметр не постоянен, то он называется изменяющейся величиной, или, еще короче, «переменной». Этот термин – «переменная величина» или попросту «переменная» — невероятно часто используется в математике.
В элементарной математике и в жизни мы часто встречаем задачи, в которых одна изменяющаяся величина зависит от другой. Простейшим видом такой закономерности является прямая пропорциональность. Например, прямая пропорциональность имеется между количеством собак и их суммарным количеством ушей. Если А – количество собак, и В — количество ушей, то мы можем написать формулу, отражающую факт прямой пропорциональной зависимости В от А:
В=2А
Число «2» и символ «А» стоят в этой формуле рядом. Это означает, что их необходимо перемножить. Конечно, можно написать так: « 2хА » или так: « 2●А », и нередко так и пишут, но для того, чтобы упростить формулы, мы договоримся, что если между символами не стоит вовсе никакого значка, то это означает, что имеется в виду умножение.
В этой записи нет словосочетания «число собак» — вместо него есть символ «А». И нет словосочетания «число ушей» — есть заменяющий его символ «В». Использование символов удобно, так как запись «число ушей равно числу два, умноженному на число собак» слишком длинная и неудобочитаемая. Использование символов делает подобные записи очень простыми и облегчает те или иные операции, которые мы можем проводить с ними. Термин «формула» и означает любую запись, сделанную в символической форме, и, конечно, имеющую какой-то определенный смысл.
Вместо символов «А» и «В» мы можем выбрать любые другие, разумеется. Исторически сложилось так, что математики чаще всего любят использовать символ «Y» (произносится «игрек») и «X» (произносится «икс»). Если переменных больше чем две, то для третьей чаще всего выбирают символ «Z» ( «зэт» ).
Y=2X
Часто вместо заглавных букв пишут прописные:
y = 2x
Знак « = » читается как «равно» или «равняется», и смысл его интуитивно понятен – он сообщает, что каждому значению икс мы должны подобрать такое значение игрек, чтобы величины в обеих частях уравнения оказались равны.
Почему эту формулу мы считаем именно выражением прямой пропорциональности? Потому что из нее видно, что если количество собак увеличить в 5, или в 10, или во сколько угодно раз, то количество ушей увеличится ровно во столько же раз. У одной собаки два уха, а у десяти собак в десять раз больше ушей, то есть двадцать. Если при увеличении чего-то в несколько раз, количество чего-то другого увеличивается во столько же раз, это и означает, что между ними существует прямая пропорциональность.
Существует ли прямая пропорциональность между игрек и икс в следующей формуле:
y = 2x + 2
Очевидно, что нет. Мы можем проверить это на конкретных примерах. Например, при х=2, у=6, а при х=4, у=10. То есть икс вырос в два раза (с двух до четырех), а игрек вырос с 6 до 10 – не в два раза. Прямой пропорциональности нет.
Теперь немного поработаем над этим уравнением. Обе части уравнения, по определению самого понятия «уравнение», равны. Если от двух равных частей отнять что-то одинаковое, равенство ведь не изменится? Если с обеих чаш уравновешенных весов снять одинаковые гири, равновесие весов не нарушится. Вычтем число 2 из обеих частей, и получим:
у-2 = 2х
Теперь левая часть уравнения прямо пропорциональна правой. Если, например, х = 1, то правая часть уравнения равна 2, а значит и левая часть должна равняться 2, то есть (у-2) должно равняться двум. При удвоенном значении х=2, значение (у-2) также удвоится и будет равняться четырем и т.д. – мы видим прямую пропорциональность. То есть тут (у-2) выступает в роли самостоятельной переменной.
Это может показаться не вполне понятным, поэтому, чтобы легче было это понимать, мы можем ввести в наше уравнение третий символ – «z». Мы можем договориться, что знаком «z» мы будем обозначать величину у, от которой отняли 2. Тогда уравнение будет записано в таком виде, из которого прямая пропорциональность видна теперь уже совершенно ясно:
z = 2x
(при этом z = y-2)
Пометки типа «при этом»… обычно опускаются, и в результате мы можем записать «систему уравнений», из которых при любом х мы легко вычислим и соответствующее ему у, и наоборот:
z = 2x
z = y-2
Рассмотрим еще один пример. Существует широко известная формула (пока неважно, как она выводится), используя которую мы можем вычислять площадь круга:
S = πR2
Здесь « π » (произносится как «пи») означает некую постоянную величину (постоянную величину часто называют одним словом «константа». Она примерно равна 3,14. Символ «S» обозначает площадь круга, а «R» — длину его радиуса (то есть длину отрезка, соединяющего центр круга с любой точкой, лежащей на ограничивающей этот круг окружности).
Запись «R2» является упрощенной записью перемножения R на R. Если нам, к примеру, потребуется четыре раза перемножить R на само себя, то мы не будем писать RRRR, а напишем более просто: R4. Согласись, что так удобней.
В формуле S = πR2 прямой пропорциональности уже нет, и это легко доказать. Предположим, что речь идет о кусте клубники. Клубника изначально заняла круг радиусом R, но через полгода она разрослась так, что радиус этого клубничного круга увеличился в два раза. Поскольку радиус увеличился в два раза, то теперь он стал равняться « 2R ». Подставим это значение в формулу, и переставляя множители так, как нам удобнее (согласно правилам умножения, мы можем переставлять множители), мы получим:
S1 = π(2R)2 = π2R2R = π4R2
Сравнивая эту формулу с первой, мы видим, что увеличение радиуса в два раза приводит к увеличению площади круга (то есть к увеличению площади земли, занятой кустом клубники) в четыре раза! (Новую площадь я обозначил как «S1», чтобы не путать с символом «S», обозначающим первоначальную площадь). Такую зависимость мы называем «квадратичной». То есть если некий параметр меняется в три или пять раз, а другой, зависящий от него и только от него параметр, меняется в девять или в двадцать пять раз соответственно, то имеет место «квадратичная зависимость». Можно не говорить каждый раз «в три раза или в пять раз или во сколько-то еще раз», а снова использовать символ. Например, пусть символ «N» будет обозначать любое число, и тогда мы сможем сказать: если некий параметр меняется в N раз, а другой, зависящий от него и только от него параметр, меняется в N2 раз, то имеет место «квадратичная зависимость».
Результаты, вычисленные с помощью этой формулы, можно свести в таблицу:
| R | 2 | 3 | 4 | 5 |
| S | 4 | 9 | 16 | 25 |
Глядя на эту таблицу, мы легко замечаем, что площадь растет намного быстрее, чем радиус – радиус вырос с двух до пяти – всего лишь на 3, а площадь – с четырех до двадцати пять, то есть на двадцать один!
Кроме таблиц, существует еще один широко распространенный способ наглядного изображения соотношения между двумя переменными – так называемый «график». Прежде чем определить — что такое график, введем понятие «осей координат».
Нарисуем горизонтальную линию. На ней отметим любую точку, и обозначим ее как «ноль». Затем отмерим от нуля один сантиметр вправо и обозначим ее как «1» — это означает, что эта точка соответствует числу «1». Еще правее на 1 сантиметр – и мы получаем точку, соответствующую числу «2», и так далее. Математики договорились, что по горизонтали мы будем откладывать числа, соответствующие переменной х. Теперь через точку ноль проведем вертикальную прямую, и отмерим от нуля один сантиметр вверх – эта точка тоже будет соответствовать числу 1, но не для переменной х, а для переменной у. Точка «ноль» называется «началом координат», а сами эти две перпендикулярные друг другу прямые называются «осями координат». Горизонтальную ось часто называют «абсциссой», а вертикальную – «ординатой».
(Можно придумать какое-нибудь дурацкое мнемоническое правило, чтобы запомнить – что есть что. Например, слово «ордината» напоминает «орден» — когда тебе вручают орден, ты стоишь совершенно вертикально, выпрямившись во весь рост, отсюда «ордината» — вертикальная ось).
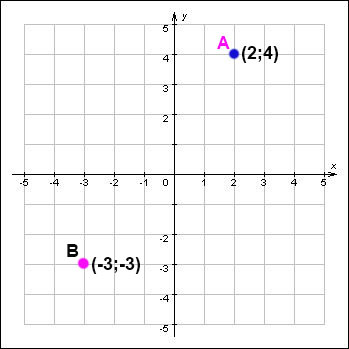
Если нарисовать точку А в произвольном месте на плоскости, на которой заданы оси координат, и через нее провести вертикальную прямую, то место пересечения этой прямой с абсциссой называется «абсциссой этой точки». Иначе говоря, «абсцисса точки графика» — это проекция точки А на ось абсцисс. Аналогично определяется «ордината точки графика». К примеру на нашей картинке абсцисса точки А равна 2, а ордината равна 4. Эта пара чисел называется «координатами» точки. Координаты точки записываются в скобках, при этом абсцисса указывается первой: А(2;4). Легко видеть что полученная пара чисел единственна, так как через заданную точку можно провести только одну единственную прямую, параллельную оси у — двух различных прямых, параллельных оси у, быть не может, значит и точка пересечения этой прямой с осью х может быть только одна.
Так как мы провели две оси координат не под произвольным углом по отношению друг к другу, а именно под прямым, то такие координаты называются «ортогональными» или, иначе, «декартовыми». Чаще всего в математике используются именно ортогональные координаты, так как они облегчают множество операций и очень наглядны. Тем не менее, можно провести ось у под любым другим углом к оси х, например под углом 45 градусов, и это тоже будет система координат, и математики и физики тоже иногда пользуются такими системами, но они уже не являются ортогональными (в будущем мы всегда будем по умолчанию использовать именно ортогональные системы координат).
Если проведенная через точку на плоскости прямая пересекает ось х справа от нуля, то мы ставим ей в соответствие некое положительное число, скажем «+5», а если слева от нуля – то отрицательное число, скажем «-4». Так же обстоит дело и с осью у — все то, что выше нуля, обозначается положительными числами, а что ниже – отрицательными. Поэтому координаты точки В мы запишем так: В(-3;-3).
Любой паре чисел х и у, таким образом, обязательно соответствует какая-нибудь единственная точка на плоскости. Обратное тоже верно – если мы на плоскости поставим какую-нибудь точку, то ей обязательно будет соответствовать единственная пара чисел. Это называется «взаимно-однозначным соответствием».
Можно сказать иначе – между множеством точек на плоскости и множеством пар чисел (x;y) существует взаимно-однозначное соответствие. Такие множества, между которыми существует взаимно-однозначное соответствие, называются «равномощными».
Рассмотрим теперь уравнение:
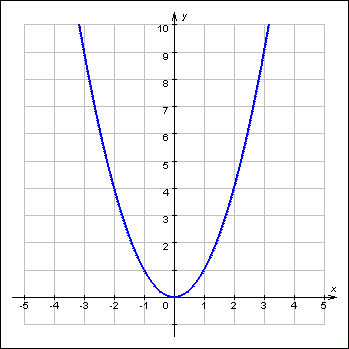
y = x2
Составим таблицу значений, удовлетворяющих этому равенству:
| х | 1 | 2 | 3 | 4 | 5 |
| у | 1 | 4 | 9 | 16 | 25 |
Пользуясь этой таблицей, мы можем нарисовать график (см.справа). По оси х отложим 1, и проведем через эту точку прямую, параллельную оси у. Затем по оси у отложим соответствующее число, то есть тоже 1. Также проведем через эту точку прямую, параллельную оси х. Эти две прямые пересекутся в точке, имеющую координаты (1;1). Таким же образом нарисуем точки с координатами (2;4), затем (3;9) и так далее.
Теперь соединим эти точки плавной (то есть без разрывов и острых углов) кривой линией, или попросту «кривой», и получим примерный график. Понятно, что если мы хотим, чтобы график был более точным, нам надо будет увеличить количество его точек. Для этого мы должны вычислить значения у для х, равных «1,5», «2.5», «3.5» и так далее, построить новые точки на графике и так далее. Чем больше точек мы возьмем, тем более точным будет график. Но и такая, даже грубо сделанная кривая, позволит нам достаточно точно представлять себе всю совокупность пар (х;у), удовлетворяющих формуле y=x2. Этот метод позволяет легко увидеть некоторые обстоятельства, которые могут быть не так очевидны, если мы перед собой видим только таблицу пар чисел. Например, мы видим, как резко возрастает у при росте х : начерченная кривая круто поднимается вверх, и это показывает, что чем больше х, тем быстрее растет у. Этот метод является, таким образом, чем-то вроде «графической таблицы», при помощи которой мы можем получить примерное значение у для каждого х и наоборот, пользуясь лишь линейкой.
Графический способ имеет то видимое преимущество, что с помощью таблицы, как правило, невозможно определить соответствие полностью – ты же не можешь нарисовать бесконечно огромную таблицу. Если я рассматриваю зависимость длины стержня от его температуры, я конечно могу выписать значения длин для температур 3 или 4 или 5 градусов. Если постараться, я могу даже расширить таблицу и выписать там значения длин для температур 3,5 или 4,5 или 5,5 градусов. Но мыслимо ли выписать еще и длины при температурах 3,455 градуса и т.д.? А вот с помощью графика я могу получить приблизительное значение длины стержня для любой температуры практически мгновенно – всего лишь проведя пару прямых.
Ну и конечно – наглядность взаимозависимости двух величин – огромное преимущество графиков.
Теперь – в конце разъяснения того, что такое график, можно дать его точное определение. Графиком функции (в системе прямоугольных или декартовых координат) называется геометрическое место точек, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции. Независимой переменной, то есть той, значение которой мы можем выбрать какую угодно по желанию, в нашем примере является х, а зависимой переменной является y, поскольку если мы задаем какую-то х, то тем самым уже совершенно точно определяем значение y. Если в нашем уравнении х=3, то y может равняться только 9, и ничему другому.
Поэтому математики говорят, что уравнение y=x2 выражает у как функцию от х. Можно сказать иначе: это уравнение задает у как функцию от х. Или так: это уравнение определяет у как функцию от х. Всё равно – можно сказать и так, и так, смысл от этого не меняется, и заключается этот смысл в том, что переменная величина у представлена как математическое выражение, как формула, в которую входит другая переменная величина х, и значение у зависит только от значения х, и не зависит больше ни от каких других переменных.
Коротко говорят об этом так: «игрек – это функция от икс». Услышав такую фразу, мы понимаем, что значение у зависит от того, какое значение принимает х, но совершенно не зависит от того, какие значения будут у каких-то там любых других переменных. Еще мы понимаем, что изменение величины х неизбежно и однозначно влечет за собой изменение величины у.
Если же перед нами уравнение типа:
y =x2 + z
то мы можем сказать, что у — это функция и от х, и от z, то есть это функция от двух переменных.
Мы можем переписать уравнение y = x2 в виде:
х =√у (икс равен квадратному корню из игрек)
и уже теперь мы можем сказать, что икс – функция от игрек, и меняя значения игрек мы будем получать каждый раз соответствующие значения для икс.
Можно сказать и по-другому: «функция – это число, которое ставится в соответствие другому числу в соответствии с заданным правилом». В нашем примере правилом является формула y=x2 , поэтому «функция от двух» будет в нашем случае «четыре» а «функция от десяти» — «сто».
До сих пор я рассматривал только взаимно-однозначные соответствия, но ситуация может быть и другой. Например, у нас в мордологове есть отдельные уровни, на которых растут фруктовые деревья – персики, груши, яблоки, папайя, манго, авокадо, помело, кумкват, мандарины, лимоны, апельсины, гранаты, и куча еще всего разного. Когда мы покупали саженцы, то выбирали такие, у которых стволы раздваивались или растраивались – так кажется красивее. Теперь пронумеруем ямки, в которых растут фруктовые деревья. Затем пронумеруем стволы. Получится, что первый, второй и третий ствол принадлежат дереву, растущему из первой ямки. Четвертый и пятый – из второй, в третьей ямке растет дерево с неразветвленным стволом номер 6 и так далее. Обозначим как у номер ямки, а как x — номер ствола, тогда у нас получится такое соотношение:
| ствол (х) | 1,2,3 | 4,5 | 6 |
| ямка (y) | 1 | 2 | 3 |
Отсюда видно, что каждому стволу соответствует одна и только одна ямка, в то время как каждой ямке могут соответствовать или один, или несколько стволов. В этом примере x также является функцией от у, так как каждому значению у соответствует одно или несколько определенных значений x. Но эта функция уже не взаимно-однозначная, как в предыдущих примерах! Она была бы взаимно-однозначной только в том случае, если бы каждому значению x соответствовало бы только одно значение у, и наоборот — каждому значению у соответствовало бы только одно значение x.
Теперь дадим более широкое определение функции: одна величина называется функцией другой величины, если каждому значению второй величины соответствует одно или несколько определенных значений первой величины. Каким образом задано это соответствие – дело десятое. Это может быть какая-то формула или совершенно произвольное решение, или соответствие может задаваться какими-то внешними причинами типа рассмотренного примера со стволами и ямками и т.д. Важно одно – есть такое соответствие или его нет. Если оно есть – значит у нас есть функция.
Например, график дежурства по кухне мы можем создать совершенно произвольно: в понедельник это один человек, во вторник – другой. Но поскольку теперь каждому дню недели соответствует один человек (или два-три, как они договорятся), то мы можем говорить о том, что нами задана функция, где каждому дню недели соответствует один или несколько человек.
Иногда слово «функция» заменяется словом «зависимая переменная». В примере с площадью круга, величина площади круга является зависимой переменной, а радиус – независимой, если мы сначала рисуем круг определенного радиуса, а затем высчитывает его площадь. Я могу выбрать радиус, какой мне захочется – он является независимой переменной, и этот выбор железобетонно определит величину зависимую – площадь круга.
Определим более точно термин «формула». Формула (или еще иначе говорят «аналитическое выражение») – это совокупность известных математических операций, то есть действий, которые производятся в определенной последовательности над числами и переменными величинами.
Например, пусть «a» — это символ, которым я обозначу действие «пройти прямо 1 метр», «b» — «повернуть на 90 градусов налево», «с» — копать вниз на 1 метр, а знак «+» обозначает совершение последующего действия. Тогда указание на место, где закопан доллар, я могу записать в виде формулы: 3а + b + 3с. Этой формулой определены обозначенные символами действия, которые производятся в определенной последовательности.
Формула – наиболее распространенный способ задания функции. Делается запись в виде равенства двух аналитических выражений, в которых участвуют две переменные величины, и по значению одной из них, которую мы принимаем за независимую переменную, мы с помощью вычислений определяем соответствующее значение другой переменной – функции.
Если у, будучи функцией х, задана формулой, то говорят, что эта формула устанавливает функциональную зависимость между у и х, или, попросту, связывают эти две величины.
Аналитический способ задания функции имеет огромные преимущества:
1) сжатость, компактность – не надо рисовать бесконечные таблицы или сложные, выверенные графики.
2) мы можем вычислить значение функции вообще для какого угодно значения независимой переменной. Например, я могу совершенно точно вычислить площадь круга радиусом 3,74322473847 метра. Попробуй сделать это с помощью графика!
3) третье преимущество – которое, наверное, сейчас будет малопонятно – это возможность изучать эту функцию с помощью аппарата математического анализа
Есть и неудобства, довольно очевидные: во-первых, слабая или вообще никакая наглядность, ну и во-вторых необходимость производить вычисления, которые могут быть такими громоздкими, что все преимущества растают без следа.
Думаю, что легко понять, что в определении понятия функции нет такого требования, чтобы при изменении независимой переменной менялась и функция. Главное – чтобы каждому рассматриваемому значению независимой переменной соответствовало определенное значение функции, а уж одно и тоже оно или разные — несущественно.
Вот это – функция?
| х | 1 | 2 | 3 | 4 | 5 |
| у | 1 | 1 | 1 | 1 | 1 |
Да, функция, ведь каждому значению «х» соответствует определенное, пусть и одинаковое, значение «у».
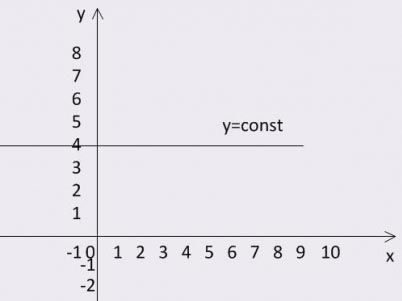
Отсюда следует интересное следствие – даже постоянную величину можно рассматривать как функцию! Ведь достаточно сказать, что любому значению переменной величины x мы ставим в соответствие, скажем, число 4 – вот такое простое правило. И число 4 станет функцией, все значения которой равны четырем при любых значениях независимой переменной х.
Осталось в этой главе ввести еще два простых термина: область определения функции и область значений функции.
«Областью определения функции» называется множество всех значений, которые может принимать переменная х, а «областью значений функции» называют множество всех значений, которые может принимать вычисляемая в соответствии с формулой переменная у.
Так, легко видеть, что в формуле
y = x2
переменная х может принимать любые значения, какие мы захотим – как положительные, так и отрицательные (и также ноль), то есть область определения данной функции – все числа. Между тем y никак не может быть отрицательным числом, так как число, возведенное в квадрат, дает или ноль или положительное число, поэтому «область значений данной функции» — это ноль и положительные числа.
Если мы напишем формулу в виде:
х =√у
то все изменится: теперь x является функцией от y, и это влечет определенные последствия. Во-первых, теперь область определения этой функции — то есть значения, которые может принимать переменная у — ограничена нулем и положительными числами, так как мы же не можем брать квадратный корень из отрицательного числа. А область значений этой функции (то есть значения, которые может принимать переменная х) может принимать любые значения. Например, если у равно 4, то х может быть и положительным числом (+2) и отрицательным (-2), так как и то и другое, возведенное в квадрат, дает 4.
Вернемся еще раз к графику. Функцию, как мы уже поняли, можно задать в виде графика – откладывай на оси абсцисс значения независимой переменной, обозначим ее как х, на оси ординат откладывай соответствующие значения функции, обозначим ее как у — и вот тебе график. Но теперь проведем обратную операцию. Просто возьмем пустую бумагу с осями координат и проведем на ней совершенно произвольную непрерывную линию. Ну линия и линия. Но теперь посмотрим на нее другими глазами. Каждая точка на линии имеет свою абсциссу и ординату. А это и означает, что эта линия является графиком некой функции! Да, любая непрерывная линия на плоскости изображает некоторую функцию, ведь если мы теперь в любом, произвольном месте того же листа бумаги построим оси координат, то теперь любая точка нашей линии будет иметь какую-то абсциссу и какую-то ординату. А это и значит, что имеет место функция.
Любая непрерывная линия является графиком функции. В подобных случаях говорят, что функция «задана графически». В физике и в технике такое происходит сплошь и рядом. Например, на сейсмостанции датчик рисует непрерывную линию сейсмической активности земной коры. Анализируя этот график, мы можем создавать разные теории строения земли. По такому же принципу работает термограф, вычерчивающий график суточной температуры.
Разумеется, задать функцию графически легко — начертил произвольно какую угодно линию, и график готов. Но это совсем не означает, что мы теперь можем легко записать ее и в аналитическом виде, то есть в виде формулы. Более того, как правило это очень сложно — подобрать такую формулу, которая бы описывала произвольно нарисованный график. Этим занимается специальная область математики.
Есть символы, которые используются в формулах чаще всего, и удобно запомнить их. Например, вместо того, чтобы писать «величина у есть некоторая функция независимой переменной величины х», пишут просто:
y = f (x)
Эта запись читается так: «игрек есть функция от икс», или еще проще: «игрек равно эф от икс».
Здесь буква f обозначает уже не величину, не какое-то определенное число, а саму зависимость, то есть закон соответствия между независимой переменной и функцией.
Если я не хочу вдаваться в детальное описание того, как именно площадь круга зависит от его радиуса, а просто хочу указать, что такая зависимость существует, то мне совершенно нет необходимости выписывать точную формулу – достаточно написать:
S = f (r)
Так как и длина окружности (L) – тоже функция ее радиуса, то мы можем написать аналогично:
L= f (r)
Эти записи выглядят совершенно одинаково несмотря на то, что аналитические выражения этих двух функций отличаются друг от друга очень сильно. И это неудобно и может вызывать невольные ошибки, поэтому – если функциональные зависимости отличаются, то математики и физики используют разные буквы, например:
S = f (r) , L= g (r)
Можно для обозначения разных зависимостей использовать одинаковые буквы, но разные индексы к ним:
S = f 1 (r) , L= f 2 (r)
И последнее для этой главы: имея конкретную формулу, которой выражена функция, мы можем вычислить, чему равно значение функции при каком-то конкретном значении независимой переменной. Например, если мы имеем формулу y = x2, то сначала мы подставляем значение переменной (скажем, пусть радиус равняется 3), производим нужные вычисления согласно формуле (возводим 3 в квадрат) и получаем значение функции (9). Это будет называться «частным значением функции». Это можно записать так:
9 = f (3)