Людям и животным свойственно «вести себя», то есть реагировать каким-то образом на внешние и внутренние «раздражители». (Любопытно – почему выбрали такой термин как «раздражитель»? Почему не «заинтересователь»? Я думаю, это произошло потому, что люди невольно отдают себе отчет в том, что доминирующее их фоновое состояние – раздражения, недовольства жизнью).
Есть собаки ласковые и есть собачащиеся. Есть люди чувственные и есть бревна. А есть функции, и они – эти функции – также имеют свое «поведение». Нет, не надо думать, что математики настолько обалдели от своих уравнений, что начинают персонифицировать математические объекты, придавая им свойства хотеть, страдать и радоваться. Просто русский язык вообще очень беден (как бы это утверждение ни злило фанатиков), и зачастую термины образуются элементарным размножением омонимического ряда. Нередко в таком подходе есть и преимущества – например, это облегчает популяризацию науки, поскольку читателям нет необходимости вдаваться в определения непонятного термина, поскольку они сразу же, хоть и очень приблизительно, понимают – о чем речь.
Приблизительно и ты понимаешь – что такое «поведение функции» — что-то вроде «ну это как она меняется», и тем не менее если ты хочешь испытать больше интеллектуального наслаждения, то целесообразно дать более точное определение.
Сначала уточним фразу «ну это как она меняется». Понятно, что один из самых очевидных способов охарактеризовать поведение функции – это значит показать – как меняется ее значение при изменении значения аргумента. При этом кажется самым простым и удобным способом такой: просто последовательно меняешь значения аргумента и смотришь, как меняется при этом значение функции. Так что для простоты примем, что независимая переменная меняется возрастая – например от нуля и дальше, причем делает она это так, что переходя от меньших значений к большим она не скачет как лошадь Пржевальского, а проходит через все свои промежуточные значения. Значит, если речь идет о функции целочисленного аргумента, то аргумент последовательно принимает целые значения, ну а если мы изучаем функцию, определенную во всех точках некоего интервала, то независимая переменная пробегает этот интервал слева направо, не пропуская ни одной точки.
Независимую переменную, которая, принимая два различных значения, принимает и любое промежуточное между ними значение, называют непрерывной. Соответственно, функцию, заданную во всех точках интервала, называют функцией непрерывного аргумента. Например, если мы говорим, что в функции непрерывного аргумента переменная непрерывна на интервале от 1 до 2, то это значит, что функция определена и при х = 1, и 2, и 0.4, и 0.05, и 0.083982928 и т.д. Везде в указанном интервале.
Теперь дадим несколько удобных определений.
Значение х, при котором функция становится равной нулю, называется нулём функции или корнем функции.
У функции, заданной формулой
у = x2 — 4
есть два «нуля функции» или «корня функции»: это числа «2» и «-2», так как, подставив вместо x любое из них, мы получим у = 0
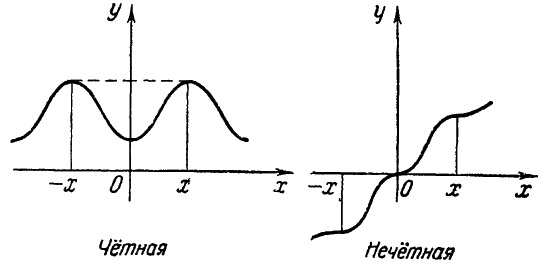
Функция у = f (x) называется четной, если при смене знака аргумента ни знак, ни значение функции не меняется. Например, функция у = x2 является четной, так как и при х=2, и при х=-2 мы неизменно получаем, что у=4. То есть у аргумента сменился знак с плюса на минус, а знак и значение функции не изменились.
Функция называется нечетной, если при смене знака аргумента меняется только знак функции, а абсолютная ее величина остается неизменной.
Например, функция у = x3 является нечетной, так как при х=2, у=8, а при х=-2 мы получаем, что у равно -8. То есть у аргумента сменился знак с плюса на минус, и знак функции тоже изменился, но восьмерка осталась восьмеркой, а не превратилась в семерку и т.д.
Легко видеть, что график четной функции всегда симметричен относительно оси 0У, а график нечетной функции всегда симметричен относительно точки 0 – начала координат.
С особенным удовольствием представляю тебе периодическую функцию :), так как роль этих функций в математике и физике огромна.
Функция у = f (x) называется периодической, если существует такое постоянное число а, не равное нулю, что от прибавления его к ЛЮБОМУ значению аргумента значение функции не меняется. В символическом виде это можно записать так: f (x+а) = f (x)
Легко доказать, что для периодической функции будет также справедлива следующая формула: f (x+2а) = f (x) , попробуй, если хочешь, доказать это сначала сама, а потом посмотри – что придумал я.
Доказательство: запишем f (x+2а) как f (x+а+а), а потом – как f ( (x+а) + а) . Мы знаем, что прибавление числа а к ЛЮБОМУ значению аргумента не приводит к изменению значения функции – значит, значение функции будет одним и тем же и при аргументе (x+а), и при аргументе (x+а) + а . Отсюда следует, что f ( (x+а) + а) = f(x+а) , а мы уже знаем из условия задачи, то f(x+а) = f (x)
Отсюда ясно, что верна и более общая формула:
f (x+kа) = f (x)
где k – произвольное целое (положительное или отрицательное) число.
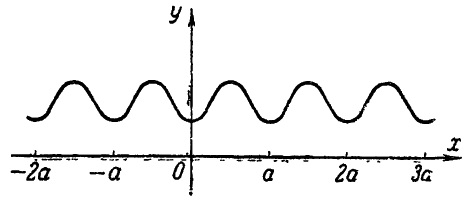
Получается, что если функция периодическая, то ее значение остается неизменным при множестве значений аргумента, которые отличаются друг от друга на определенную величину а. Мы знаем, что значение периодической функции остается тем же, если к аргументу прибавить а или 2а и т.д. Наименьшее из чисел, добавление которого к любому значению аргумента не меняет значения функции, называется периодом функции.
Изучение периодических функций упрощается тем фактом, что она ведет себя совершенно одинаково в любом интервале значений аргумента, длина которого равна периоду функции.
Например, возьмем какую-нибудь периодическую функция с периодом, равным а. Посмотрим на её график. Возьмем тот кусок её графика, который соответствует пробеганию независимой переменной от 3 до 4, скажем. Так как эта функция является периодической с периодом, равным а, то это и значит по определению, что значение функции при аргументе, равным 3+а в точности такое же, каково оно было при аргументе равном 3. При x равном 4+а , значение функции в точности такое же, каким оно было при x равном 4. И все то же самое касается всех точек на этом интервале. Значение функции при аргументе, равным 3.4+а в точности такое же, каково оно было при аргументе равном 3.4 и так далее. Это и значит, что функция на любом интервале значений аргумента в точности такая же, как на интервале, который расположен на а левее или правее.
Это легко понять, просто посмотрев на график какой-нибудь периодической функции, а также вспомнив, что f (2) = f (а+2) и т.д., то есть после того, как аргумент перевалит за значение (а+2), значения функции начнут повторяться в точности так же, как это уже было, когда аргумент переваливал за 2.
Термины «возрастание функции» и «убывание функции» тоже, в общем, интуитивно понятны, но все же необходимо дать этим терминам математическое определение, так как если определение такое есть, то, пользуясь им, можно находить ответы на многие вопросы, которые в противном случае становятся неприемлемо расплывчатыми. Интересно, что именно точность определений как в математике, так и в других науках является сама по себе двигателем развития этих наук, поскольку – когда есть точное определение, всегда можно его немного изменить и спросить себя – «а вот если так будет, то что у нас получится»? Когда-то Лобачевский задал себе вопрос – а что, если мы рассмотрим такую ситуацию, когда параллельные прямые пересекаются? Ему показалось, что аксиома параллельности Евклида (согласно которой на плоскости через точку, не лежащую на данной прямой, проходит только одна прямая, не пересекающая данную) является совершенно произвольным ограничением, которая не может отражать полностью свойства пространства. И он предложил другую аксиому: «на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Ну ведь, казалось бы, чушь! Но это не чушь, это математика. Если бы Евклид говорил о параллельных прямых расплывчато, то и развить его идеи было бы невозможно. Но вот дано точное определение, после чего можно задаться вопросом – а что, если построить математику, опирающуюся на совсем другую аксиому? И в итоге мы получаем довольно абстрактную ветвь математики. Абстрактную, поскольку пока что мы не понимаем – как это может быть приложено к нашей жизни. Но математика, во-первых, наука не прикладная – я получаю удовольствие от самого процесса математического мышления, а не от того, что кто-то к чему-то ее применил. И кроме того, наши знания о мире постоянно расширяются, и когда физики пришли к необходимости принять теорию криволинейного пространства, геометрия Лобачевского нашла свое применение.
(Лобачевского как раз и не поняли, оценивая его труд, например, в таких выражениях: «Как можно подумать, чтобы Лобачевский, ординарный профессор математики, написал с какой-нибудь серьёзной целью книгу, которая немного бы принесла чести и последнему школьному учителю? Если не учёность, то по крайней мере здравый смысл должен иметь каждый учитель, а в новой геометрии нередко недостает и сего последнего». И умер Лобачевский в нищете и безысходности, но если у тебя возникла к нему жалость, подумай о том, что его жена родила от него 18 детей. Это как же надо относиться к своей жене, чтобы свести ее на уровень свиноматки? Да и имея 18 детей трудно так извернуться, чтобы не жить в крайней нищете, так что это еще и безразличие к своим детям.
Итак, функция называется возрастающей (в данном интервале значений аргумента), если бОльшим значениям независимой переменной в этом интервале соответствуют бОльшие значения функции. Ну и соответственно, функция называется убывающей, если бОльшим значениям независимой переменной в этом интервале соответствуют меньшие значения функции.
То, что записано выше словами, можно записать и в более строгом виде – кому-то такая запись покажется более трудной для восприятия, но на самом деле это вопрос привычки, и в виде формул математические фразы воспринимать в конечном счете быстрее и удобнее.
f (x) возрастает в интервале (a,b), если для всех значений x1 и x2 , удовлетворяющих условию a ˂ x1˂ x2 ˂ b имеет место неравенство: f (x1) ˂ f (x2), и убывает, если f (x1) > f (x2).
Прочла определение? Оно понятно? Теперь оторвись от текста и попробуй произнести это определение по памяти. Уверен, что это тебе дастся не без труда. Это и означает, что твое понимание пока что плавающее, легко ускользающее. Попробуй повторить: снова прочти эту фразу, медленно, обдумывая каждое слово и каждый знак, и потом снова попробуй произнести это определение на память. Я уверен, что когда ты сможешь произнести определение по памяти, то к этому времени будешь гораздо четче и яснее его понимать. Даже если одну незначительную деталь упустить из этого определения, оно уже станет неточным и может впоследствии приводить к ошибкам.
Визуально представить графики возрастающей и убывающей функций очень легко. Если рассматривать график функции слева направо, что соответствует росту значений аргумента x, то для возрастающей функции точка графика поднимается вверх (линия АВ на схеме ниже), а для убывающей – опускается вниз (линия CD).
Как мы уже знаем, участки графика функции на разных интервалах независимой переменной могут быть совершенно разными, так же как разными могут быть и формулы, определяющие эту функцию на разных интервалах независимой переменной. В частности, на одном интервале функция может быть возрастающей, а на другом – убывающей.
Соответственно, интервал независимой переменной, в котором функция возрастает, называется интервалом возрастания функции. Как интервал возрастания, так и интервал убывания называются «интервалом монотонности функции», а функция в этом интервале называется «монотонной функцией». То есть монотонная на данном интервале функция – это такая функция, которая на этом интервале или только возрастает, или только убывает.
Еще одно простое определение, которое настолько просто, что не потребует ни графиков, ни формул: значение функции, большее или меньшее всех других ее значений в некотором интервале, называется наибольшим, или, соответственно, наименьшим значением функции в этом интервале.
Еще один простой термин, который пригодится в будущем: функция, заданная равенством:
у = а1 f1 (x) + а2 f2 (x) + а3 f3 (x) +… + аn fn (x)
где а1, а2 … аn – постоянные, называется линейной комбинацией функций f1 (x), f2 (x) … fn (x). Пока что это определение можно просто понять и запомнить, а потом мы еще часто встретимся с линейными комбинациями функций.