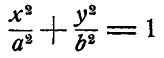Не то, чтобы вопрос классификации функций был очень уж важен для математики, но… что такое «важность для математики»? Для математики важно то, от чего я могу получать удовольствие, изучая ее. Интересно – получал ли швед Карл Ингемарссон удовольствие, когда придумывал свою систему классификации растений и животных? Когда, согласно ей, описал десятки тысяч (!!) видов растений и животных? Ну, это вопрос для историков. Как, ты не знаешь, кто такой Карл Ингемарссон?? Это великий натуралист, известный всему миру, а ты его не знаешь?? Ну ладно, ладно. На самом деле его отец – Нильс Ингемарссон, заменил свою настоящую фамилию латинским псевдонимом — для солидности, ведь тогда он поступил в университет, и в качестве псевдонима выбрал слово, связанное с их родовым символом – большой шведской липой (lind), так что его сын Карл стал впоследствии всем известен под фамилией Линней.
Линней мог получать удовольствие, а мог трудиться, как заведенный, лишь для того, чтобы стать членом Парижской Академии наук и хвастаться этим среди росхультчан и уппсальчан. Для меня сейчас интересно другое – можно ли было испытывать удовольствие от составления классификации и последующим классифицированием живых существ? Я уверен, что да – можно, потому что я и сам получаю такое удовольствие. Я получал его, когда создавал классификацию озаренных восприятий. Я получаю его, когда разбираюсь в классификации функций, растений, жуков и гномодомов для мордопоселений. Классификация – это работа, состоящая, во-первых, в различении, так как необходимо различить и обозначить те самые отличительные признаки, которые и отличают один вид от другого, и во-вторых – это работа по выявлению этих отличий в реальных существах или объектах. То есть тут работает и различающее сознание, и интеллект, и как то, так и другое приносит удовольствие, когда ты этим занимаешься в свое… эээ… удовольствие, а не из-под палки.
1. Различить явные и неявные функции совсем несложно. Это различение касается только таких функций, которые заданы аналитически (если забыла – что это такое – посмотри – намного приятнее совершенно точно понимать – о чем идет речь, чем иметь расплывчатое представление). Функция у аргумента х называется явной, если прямо указывается аналитическое относительно х выражение, которому равна у.
Например, функция y = 2x является явной, так как в этой формуле прямо указано – что нужно сделать со значением х, чтобы получить значение у – взял, подставил, посчитал – готово. А вот – уравнение эллипса:
Эта функция задана в неявном виде, так как если мы возьмем некое значение х и подставим его в формулу, то значение у придется дополнительно вычислять с помощью аналитических преобразований этой формулы – сначала придется сделать так, чтобы с одной стороны уравнения остался только у, а все остальное было с другой стороны. И зачастую совсем непросто произвести такую операцию выделения у в чистом виде! Например, уравнение:
у3 + 2ху — х3 = 0
тоже определяет у как функцию х, но чтобы найти значение у при данном х, требуется выделить у в чистом виде, то есть, иначе говоря, решить уравнение третьей степени, что очень непросто.
2. Есть еще один способ выделить определенный вид функций, заданных аналитически (то есть в виде формулы). Есть так называемые алгебраические функции. Термин «алгебраические операции» означает очень простую вещь – алгебраической операцией является любая совокупность пяти операций: сложения, вычитания, умножения, деления и возведения в степень с рациональным показателем (то есть и взятие корня). Функция, значения которой можно получить, производя над независимой переменной конечное число алгебраических действий, называется «явной алгебраической».
Частный случай алгебраической функции – «рациональная функция». Функция называется рациональной, если ее значения можно получить, производя над независимой переменной конечное число лишь четырех операций: сложения, вычитания, умножения и деления (то есть тут не должно быть взятия корней из независимой переменной).
Ну и теперь легко понять – что такое «иррациональная функция» — это такая алгебраическая функция, которая не является рациональной, то есть такая, в аналитическом выражении которой присутствует взятие корня из независимой переменной.
Например, функция:
у=√х
является иррациональной.
Еще одна разновидность – «целые функции». Рациональная функция называется целой, если для её определения не употребляется деление на выражение, включающее в себя независимую переменную. То есть, грубо говоря, независимая переменная х не должна стоять в знаменателе, тогда функция будет целой.
Существует другой термин для обозначения целой рациональной функции – он широко известен. Этот термин – «многочлен» или «полином». Уверен, что слово «многочлен» всем знакомо еще со школьных времен, но никто, кроме истинных математиков-любителей (иногда среди них попадаются и профессионалы), не имеет никакого представления о том – что это такое – многочлен. Обычно представляют просто кучу разных выражений, сваленных воедино, но теперь ты точно знаешь, что многочлен – это, во-первых, явная функция, то есть у должен быть выделен в явном виде и стоять с одной стороны знака равенства. Во-вторых, это рациональная функция, то есть с другой стороны знака равенства не должно быть квадратных и прочих разных корней. И в-третьих, независимая переменная не должна быть в знаменателе.
Можно заметить, что одночлен тоже является частным случаем многочленов – просто там количество членов равно единице, так что уравнение у = 2х также является, вообще говоря, многочленом.
Полиномы играют огромную роль в математике, поэтому целесообразно сразу разобраться – кто они такие.
Любой многочлен всегда можно разложить по убывающим или возрастающим степеням независимой переменной, то есть сначала мы группируем все х, затем – х2, затем х3 и так далее. Таким образом скомпонованная формула будет выглядеть так:
у = а0xn + а1xn-1 + а2xn-2 +… + аn-1x + аn
здесь а0, а1, а2 и т.д. – коэффициенты, то есть постоянные величины.
Это довольно очевидно, что многочлен можно вот так разложить по степеням, так как если, допустим, в формуле есть два элемента: аx2 + bx2, то вынося x2 за скобки, мы как раз и получим (a+b)x2, после чего (a+b) обозначаем как а0.
Если функция не является алгебраической, то она называется «трансцендентной». Так функция:
у = sin (x)
является трансцендентной.
3. Еще есть один очень простой способ разделить функции на два вида. Если каждому значению независимой переменной соответствует только одно определенное значение функции, то такая функция называется однозначной. Если два или больше – многозначной. Это просто.
Однозначность функции легко видна на ее графике. Геометрически однозначность функции означает, что если в любом месте провести прямую, параллельную оси ординат, то она пересечет график функции только один раз. А если она пересечет график более одного раза – значит это уже многозначная функция, так как одному значению независимой переменной х соответствует более одного значения у.
Бывает и так, что в каком-то диапазоне значений х функция однозначна (то есть ее график пересекается вертикальной прямой лишь один раз), а в других диапазонах значений х – многозначна. В таком случае, мы можем представить всю функцию в целом как комбинацию двух функций – однозначной на одном диапазоне значений х, и многозначную на остальных. Первую функцию при этом называют «однозначной ветвью многозначной функции».